Spin Qubits and Quantum Dot Circuits

Our research on gate-controlled quantum dots focuses on the experimental implementation of spin qubit arrays in various material systems with the aim of understanding fundamental interactions in solids and deriving applications in quantum simulations and quantum computing. Key resources include access to high-quality quantum materials, nanofabrication facilities (both in-house and external), and the ability to couple quantum dots locally via gate-voltage pulses and over larger distances via superconducting resonators.

We study spin qubits in several semiconductor material platforms to extend this research field toward larger and well-controlled qubit networks, as well as to investigate fundamental questions in condensed matter physics [1]. For example, gallium-arsenide (GaAs) heterostructures allow us to study in great detail the dynamics of nuclear spins [2,3] and electron-electron correlations [4,5], whereas spin qubits made from isotopically-purified silicon-28 (²⁸Si) display excellent coherence times and provide a natural quantum material platform compatible with industrial fabrication and engineering [6]. To learn more about our involvement with quantum large-scale integration in silicon, visit the QLSI homepage.

Arrays of quantum dots not only provide a suitable platform for quantum computing, but can also simulate the mechanics of the tiniest building blocks of the universe. Indeed, quantum dots display discrete electronic states similar to quantum states of atoms and molecules, making it possible to accelerate the understanding of biochemical processes and, eventually, lead to the development of new medicine.

While all activities involve a fruitful collaboration between experimental physics and theory, we are also exploring synergies with computer science in optimization, automation, and machine learning [7,8]. This enables us to complement a deepening understanding of spin phenomena with increasing control complexity in larger and larger quantum-dot circuits.

Our experiments are performed in dilution refrigerators below 100 mK and in the presence of magnetic fields up to 6 T, exploiting high-frequency control and measurement techniques that may find applications in other research fields, for instance, Topological Quantum Systems.

Example of a spin-qubit circuit implemented in gallium-arsenide (GaAs) comprising 13 quantum dots [9]. Each of the 8 quantum dots marked by a yellow circle can be occupied by a single electron, by appropriate application of gate voltages (red lines). Four larger quantum dots (green circles) serve as sensor dots that are read out by radio-frequency reflectometry (blue lines) [10]. The elongated quantum dot in the center (orange) serves as a quantum mediator [11]. The simplest encoding of one qubit are the two spin states of a single electron [1]. Another encoding uses the spin singlet and (unpolarized) spin triplet state of a two-electron double dot, which can be used to detect with great sensitivity the dynamics of nuclear spins in the GaAs crystal [2, 3]. Triple-dot encodings allow universal single-qubit rotations using only gate-voltage pulses, including the use of symmetry points that potentially prolong qubit coherence [12]. Quantum-dot networks programmed by gate voltages are fantastic devices to study a range of questions in condensed matter physics, as they can be re-configured in situ to enable different functionalities.

General purpose cryogenic sample holder provided by QDevil with a spin-qubit chip wirebonded to a PCB chip carrier, allowing the application of low-frequency and high-frequency signals for the control of gate voltages and the readout of qubits.

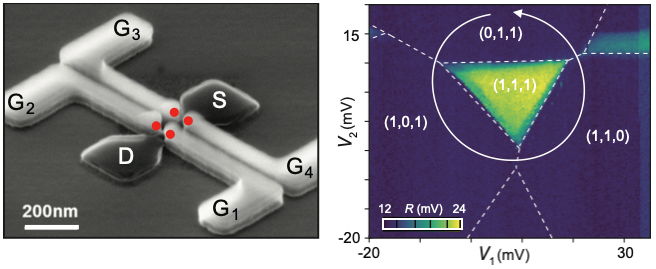
Example of single-electron operations in a silicon spin-qubit device fabricated entirely in an industrial microelectronics foundry [6]. Left: Four independent gate electrodes (light gray) touch an undoped silicon channel (dark gray), allowing the creation of up to four quantum dots (red dots) in this transistor-like device. Right: The reflectometry signal R collected from one quantum dot reveals the single-electron charge occupation (1,1,1) of the other three quantum dots as a function of detuning voltages. By executing a gate-voltage loop along the shown trajectory, from (0,1,1) via (1,0,1) and (1,1,0) back to (0,1,1), we can exchange two isolated electrons by spatial permutation, which may find applications in permutation-based quantum algorithms.

References cited:

_{[1] Chatterjee, A., Stevenson, P., De Franceschi, S., Morello, A., de Leon, N. P., & Kuemmeth, F. (2021). Semiconductor qubits in practice. Nature Reviews Physics, 3(3), 157–177. https://doi.org/10.1038/s42254-021-00283-9}

_{[2] Notch filtering the nuclear environment of a spin qubit, F. K. Malinowski, F. Martins, P. D. Nissen, E. Barnes, M. S. Rudner, S. Fallahi, G. C. Gardner, M. J. Manfra, C. M. Marcus, F. Kuemmeth, Nature Nanotechnology 12, 16 (2016). https://doi.org/10.1038/nnano.2016.170}

_{[3] Spectrum of the Nuclear Environment for GaAs Spin Qubits, F. K. Malinowski, F. Martins, Ł. Cywiński, M. S. Rudner, P. D. Nissen, S. Fallahi, G. C. Gardner, M. J. Manfra, C. M. Marcus, F. Kuemmeth, Phys. Rev. Lett. 118, 177702 (2017). https://doi.org/10.1103/PhysRevLett.118.177702}

_{[4] Negative spin exchange in a multielectron quantum dot, F. Martins, F. K. Malinowski, P. D. Nissen, S. Fallahi, G. C. Gardner, M. J. Manfra, C. M. Marcus, F. Kuemmeth, Phys. Rev. Lett. 119, 227701 (2017). https://doi.org/10.1103/PhysRevLett.119.227701}

_{[5] Spin of a multielectron quantum dot and its interaction with a neighboring electron, K. Malinowski, F. Martins, T. B. Smith, S. D. Bartlett, A. C. Doherty, P. D. Nissen, S. Fallahi, G. C. Gardner, M. J. Manfra, C. M. Marcus, F. Kuemmeth, Phys. Rev. X 8, 011045 (2018). https://doi.org/10.1103/PhysRevX.8.011045}

_{[6] Ansaloni, F., Chatterjee, A., Bohuslavskyi, H., Bertrand, B., Hutin, L., Vinet, M., & Kuemmeth, F. (2020). Single-electron operations in a foundry-fabricated array of quantum dots. Nature Communications, 11(1), 6399. https://doi.org/10.1038/s41467-020-20280-3}

_{[7] Estimation of Convex Polytopes for Automatic Discovery of Charge State Transitions in Quantum Dot Arrays, O. Krause, T. Rasmussen, B. Brovang, A. Chatterjee, F. Kuemmeth, arXiv:2108.09133 (2021). https://arxiv.org/abs/2108.09133}

_{[8] Chatterjee, A., Ansaloni, F., Rasmussen, T., Brovang, B., Fedele, F., Bohuslavskyi, H., Krause, O., & Kuemmeth, F. (2021). Autonomous estimation of high-dimensional Coulomb diamonds from sparse measurements. ArXiv:2108.10656 [Cond-Mat]. http://arxiv.org/abs/2108.10656}

_{[9] Fedele, F., Chatterjee, A., Fallahi, S., Gardner, G. C., Manfra, M. J., & Kuemmeth, F. (2021). Simultaneous Operations in a Two-Dimensional Array of Singlet-Triplet Qubits. PRX Quantum, 2(4), 040306. https://doi.org/10.1103/PRXQuantum.2.040306}

_{[10] Fast Charge Sensing of Si/SiGe Quantum Dots via a High-Frequency Accumulation Gate, C. Volk, A. Chatterjee, F. Ansaloni, C. M. Marcus, F. Kuemmeth, Nano Letters 19, 5628 (2019). https://doi.org/10.1021/acs.nanolett.9b02149}

_{[11] Fast spin exchange across a multielectron mediator, F. K. Malinowski, F. Martins, T. B. Smith, S. D. Bartlett, A. C. Doherty, P. D. Nissen, S. Fallahi, G. C. Gardner, M. J. Manfra, C. M. Marcus, F. Kuemmeth, Nature Communications 10, 1196 (2019). https://doi.org/10.1038/s41467-019-09194-x}

_{[12] Symmetric Operation of the Resonant Exchange Qubit, F. K. Malinowski, F. Martins, P. D. Nissen, S. Fallahi, G. C. Gardner, M. J. Manfra, C. M. Marcus, F. Kuemmeth, Phys. Rev. B 96, 045443 (2017). https://doi.org/10.1103/PhysRevB.96.045443}

Center for Quantum Devices

Spin Qubits and Quantum Dot Circuits

References cited: